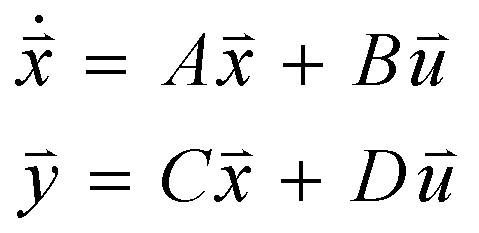Introduction

In order to gain a perspective for robust control, it is useful to examine some basic concepts from control theory. Control theory can be broken down historically into two main areas: conventional control and modern control. Conventional control covers the concepts and techniques developed up to 1950. Modern control covers the techniques from 1950 to the present. Each of these is examined in this introduction.

Conventional control became interesting with the development of feedback theory. Feedback was used in order to stabilize the control system. One early use of feedback control was the development of the flyball governor for stabilizing steam engines in locomotives. Another example was the use of feedback for telephone signals in the 1920s. The problem was the transmission of signals over long lines. There was a limit to the number of repeaters that could be added in series to a telephone line due to distortion. Harold Stephen Black proposed a feedback system that would use feedback to limit the distortion. Even though the added feedback sacrificed some gain in the repeater, it enhanced the overall performance. Refer to [Bennet96] for more historical treatment of control theory.

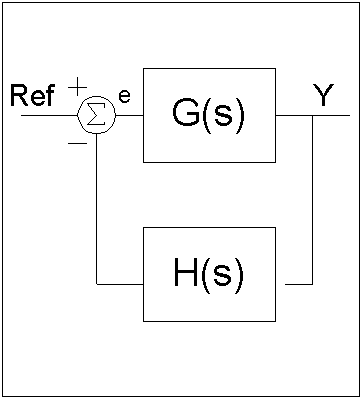
Conventional control relies upon developing a model of the control system using differential equations. LaPlace transforms are then used to express the system equations in the frequency domain where they can be manipulated algebraically. Figure 1 shows a typical control loop. The input to the system is some reference signal, which represents the desired control value. This reference is fed through a forward transfer function G(s) to determine the plant output, y. The output is fed back through a feedback transfer function, H(s). The feedback signal is subtracted from the reference to determine the error signal, e. Further control is based on the error signal. Therefore, the system serves to bring the output as close as possible to the desired reference input. Due to the complexity of the mathematics, conventional control methods were used mostly for Single-Input-Single-Output (SISO) systems. Refer to [Oppenheim97] for an introduction to conventional control techniques.

Figure 1: Typical Control Loop

One development that was key to future developments in robust control was the root-locus method. In the frequency domain, G(s) and H(s) were expressed as ratios of polynomials in the complex frequency variable, s. Nyquist, Bode and others realized that the roots of the denominator polynomial determined the stability of the control system. These roots were referred to as "poles" of the transfer functions. The location of these poles had to be in the left half-plane of the complex frequency plot to guarantee stability. Root locus was developed as a method to graphically show the movements of poles in the frequency domain as the coefficients of the s-polynomial were changed. Movement into the right half plane meant an unstable system. Thus systems could be judged by their sensitivity to small changes in the denominator coefficients.

Modern control methods were developed with a realization that control system equations could be structured in such a way that computers could efficiently solve them. It was shown that any nth order differential equation describing a control system could be reduced to n 1st order equations. These equations could be arranged in the form of matrix equations. This method is often referred to as the state variable method. The canonical form of state equations is shown below, where x is a vector representing the system "state", is a vector representing the change in "state", u is a vector of inputs, y is a vector of outputs, and A, B, C, D are constant matrices which are defined by the particular control system.

Modern control methods were extremely successful because they could be efficiently implemented on computers, they could handle Multiple-Input-Multiple-Output (MIMO) systems, and they could be optimized. Methods to optimize the constant state matrices were developed. For instance a spacecraft control system could be optimized to reach a destination in the minimum time or to use the minimum amount of fuel or some weighted combination of the two. The ability to design for performance and cost made these modern control systems highly desirable. There are many books covering the mathematical details of modern control theory. One example is [Chen84]. A lighter overview of the key developments in modern control can be found in [Bryson96]

Key Concepts

Robust Control Definition

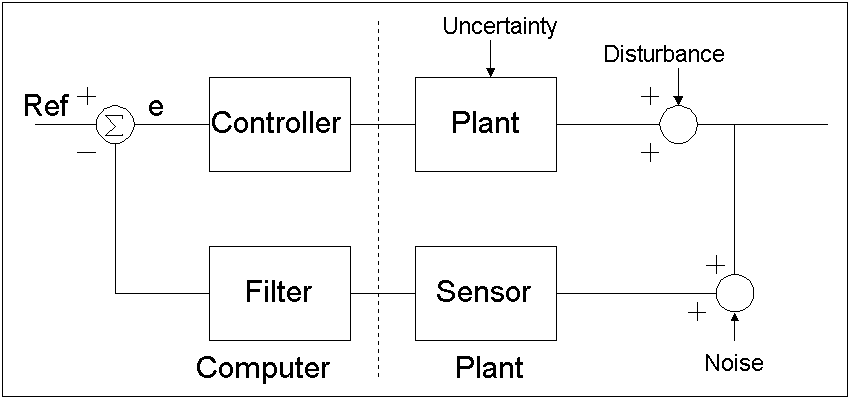
From [Chandraseken98], "Robust control refers to the control of unknown plants with unknown dynamics subject to unknown disturbances". Clearly, the key issue with robust control systems is uncertainty and how the control system can deal with this problem. Figure 2 shows an expanded view of the simple control loop presented earlier. Uncertainty is shown entering the system in three places. There is uncertainty in the model of the plant. There are disturbances that occur in the plant system. Also there is noise which is read on the sensor inputs. Each of these uncertainties can have an additive or multiplicative component.

Figure 2: Plant control loop with uncertainty

The figure above also shows the separation of the computer control system with that of the plant. It is important to understand that the control system designer has little control of the uncertainty in the plant. The designer creates a control system that is based on a model of the plant. However, the implemented control system must interact with the actual plant, not the model of the plant.

Effects of Uncertainty

Control system engineers are concerned with three main topics: observability, controllability and stability. Observability is the ability to observe all of the parameters or state variables in the system. Controllability is the ability to move a system from any given state to any desired state. Stability is often phrased as the bounded response of the system to any bounded input. Any successful control system will have and maintain all three of these properties. Uncertainty presents a challenge to the control system engineer who tries to maintain these properties using limited information.

One method to deal with uncertainty in the past is stochastic control. In stochastic control, uncertainties in the system are modeled as probability distributions. These distributions are combined to yield the control law. This method deals with the expected value of control. Abnormal situations may arise that deliver results that are not necessarily close to the expected value. This may not be acceptable for embedded control systems that have safety implications. An introduction to stochastic control can be found in [Lewis86].

Robust control methods seek to bound the uncertainty rather than express it in the form of a distribution. Given a bound on the uncertainty, the control can deliver results that meet the control system requirements in all cases. Therefore robust control theory might be stated as a worst-case analysis method rather than a typical case method. It must be recognized that some performance may be sacrificed in order to guarantee that the system meets certain requirements. However, this seems to be a common theme when dealing with safety critical embedded systems.